drw intern oa 25 summer | DRW QR Intern OA | drw Interview Assist | OA Guarantee

This year DRW The 2025 Summer Quant/QR Intern OA has been released one after another! As in previous years, the overall difficulty is still not low, the number of questions is on the large side, and the time pressure is quite obvious. The scope of examination mainly focuses on mathematical reasoning, probability statistics, brain teasers and programming questions. Many students will be a bit panicked when they first get the questions, not knowing how to allocate time, but also easy to lose points in the details. Our side has also helped students successfully take the DRW OA, and students who have experienced it say that if there is a point of view, the efficiency and correctness are completely two levels.

Main business

DRW's business focuses on three main areas.

1. Liquidity Providing
2. Risking Taking
3. Latency Sensitive Trading

DRW's OA is still quite difficult, 6 math questions in 45 minutes, time is still very tight, below together with the DRW intern oa 25 summer questions.

Issue 1

The probability that the coin is heads up is 0.8 and tails up is 0.2, so if you choose heads, the probability that each flip will be heads is 0.8. In 100 flips, the expected number of heads is 100 × 0.8 = 80, and each heads will yield$80.

Issue 2

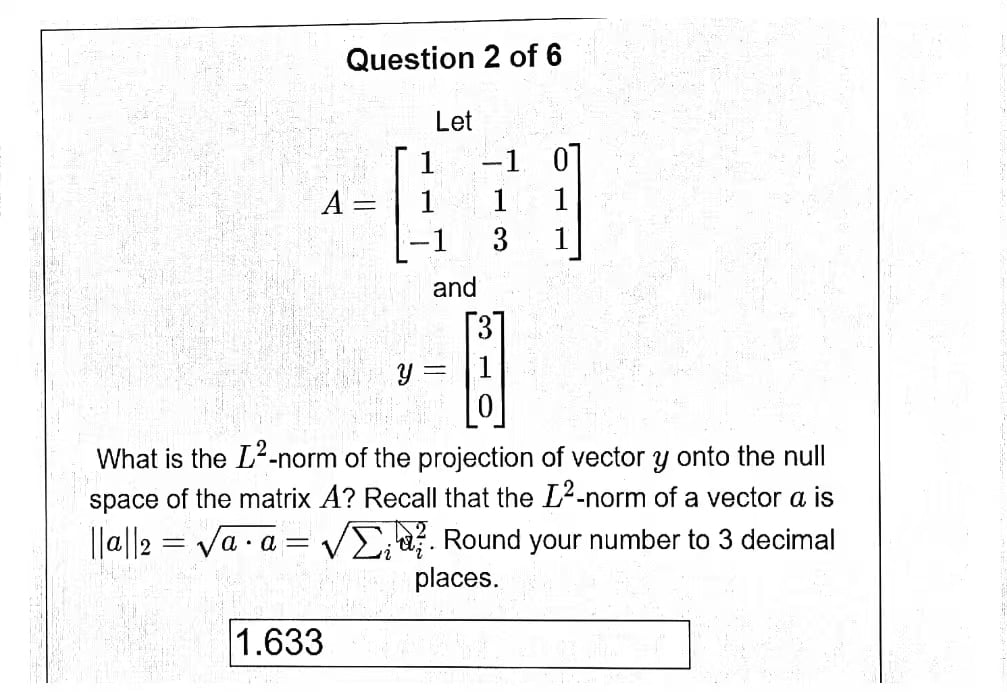
First determine the zero space of the matrix A, then compute the projection of y into this space, and finally find the L2-paradigm of this projection.

Question 3

The question asks to find a constant c to minimize the quantization error, which can be solved by writing Python code directly to set the formula:

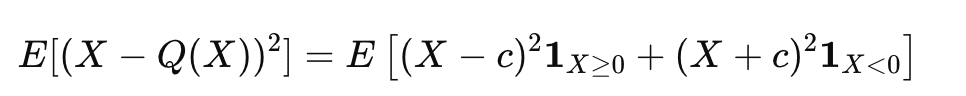
from scipy.optimize import minimize
from scipy.stats import norm

# Define the objective function to be minimized
def quantization_error(c).
    # Parameters of the normal distribution
    mean = 0
    variance = 3
    std_dev = variance**0.5

    # Error Calculation
    # For x >= 0, compute (x - c)^2, for x < 0, compute (x + c)^2
    error_positive = lambda x: (x - c)**2 * norm.pdf(x, loc=mean, scale=std_dev)
    error_negative = lambda x: (x + c)**2 * norm.pdf(x, loc=mean, scale=std_dev)

    integral_positive = norm.expect(error_positive, loc=mean, scale=std_dev, lb=0, ub=np.inf)
    integral_negative = norm.expect(error_negative, loc=mean, scale=std_dev, lb=-np.inf, ub=0)

    return integral_positive + integral_negative

result = minimize(quantization_error, x0=0.5)
optimal_c = round(result.x[0], 3)
optimal_c

Question 4

The probability of throwing a thrown face after seeing 6 different faces is 6/7. Let E be the total expected number of times, and solve the recursive equation to obtain the recursive formula:

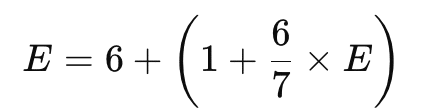
Question 5

Here each time a coin is tossed, it moves forward 1 or 2 steps depending on the result of the coin's heads and tails. We need to calculate P_n, i.e., "the probability of finally reaching the nth step", and in particular, find P₄WP and P₁₀value, and then calculate 1000(p₄+p₁₀).

Reference

DRW intern oa 25 summer | Acreage

Summer 2025 Quant Internships

With our written test assistance, the candidate successfully completed the OA for DRW Intern and got the interview, if you also need OA assistance, interview assistance, substitute interview, pleasecontact us.

ProgramHelp

See Full Bio