Intuit Recently, I have started to focus on OA again. This time it is 26 NG SDE. There are three questions in total, the programming + SQL + Bash mixed one. The overall feeling is: not tricky, the test is all about "whether you have really written code." Intuit is actually a very familiar company, and the style of writing has not changed much over the years. As long as you don't panic, you have enough time. This set of mine is a one-time use. Anyone related to OA/VO can also communicate with each other, and the results can be checked. Here I will briefly explain the core ideas of the three questions.
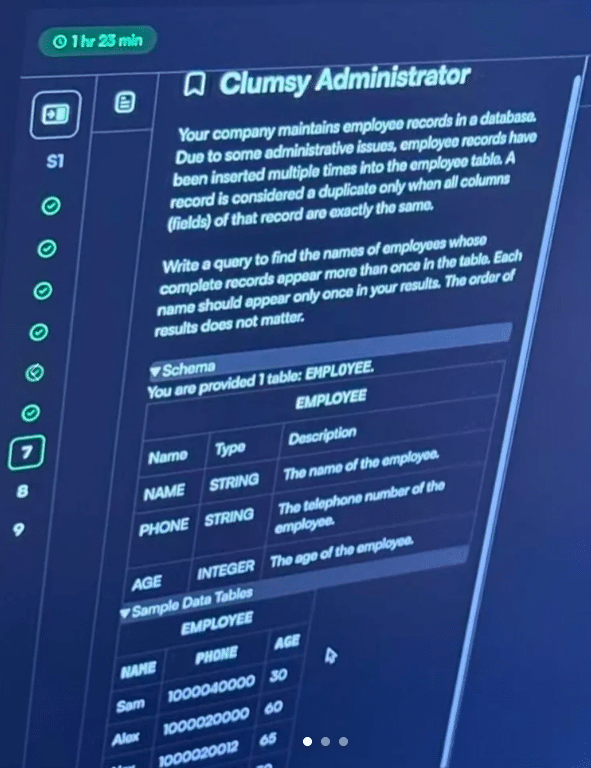
Q1: Repeated user queries in the database
Introduction to the topic
Given a user table, it is required to find duplicate user records that are exactly the same on three specified attributes and output the names of these duplicate users. Only when these three attributes are the same at the same time are the same type of repeat users considered.
Problem-solving ideas
This is a standard grouped question to eliminate duplicates. The core lies in whether the grouping conditions are accurate. Directly follow the three attributes given in the question GROUP BY,pass HAVING COUNT(*) > 1 Filter out the groups that actually have duplicates. Then extract the corresponding user names from these repeated groups, deduplicate the names and then output them. The whole question does not require complex subqueries. The key is not to split the grouping conditions incorrectly.
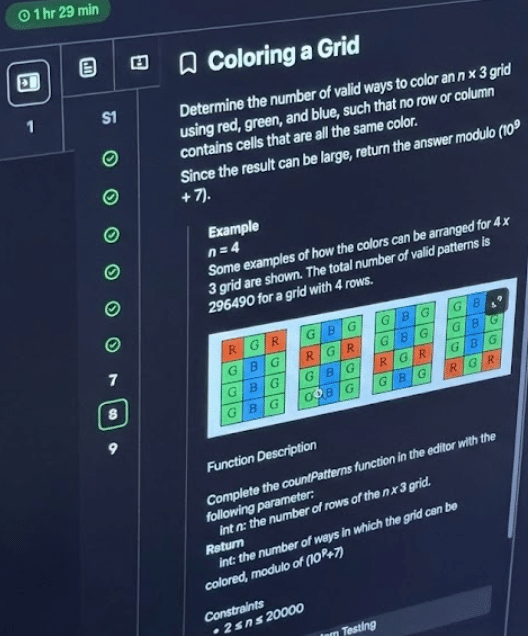
Q2: Number of color arrangement schemes for n rows and 4 columns of squares
Introduction to the topic
Given a grid with n rows and 4 columns, the colors of the 4 grids in each row must be different from each other. At the same time, it is required that in the entire square, the same color cannot appear in the same column, and the total number of arrangement schemes that meet the conditions is found.
Problem-solving ideas
This question is essentially a combinatorial counting problem and requires the use of the inclusion-exclusion principle. Let’s start with the simplest case: the 4 positions in each row are all different colors, and the arrangement of a row is 4!, which is 24 ways. N rows are independent of each other, and the total number of solutions is 24 to the nth power.
Next, deal with the illegal situation: the same column has the same color. Through the principle of inclusion and exclusion, the number of the same options in any one column is subtracted in turn, then the number of the same options in any two columns is added back, and finally the number of the same options in any three columns is subtracted. Calculated in this order, the result is the final number of legal solutions. This question is not about complicated calculations, but about whether the constraints can be clearly broken down.
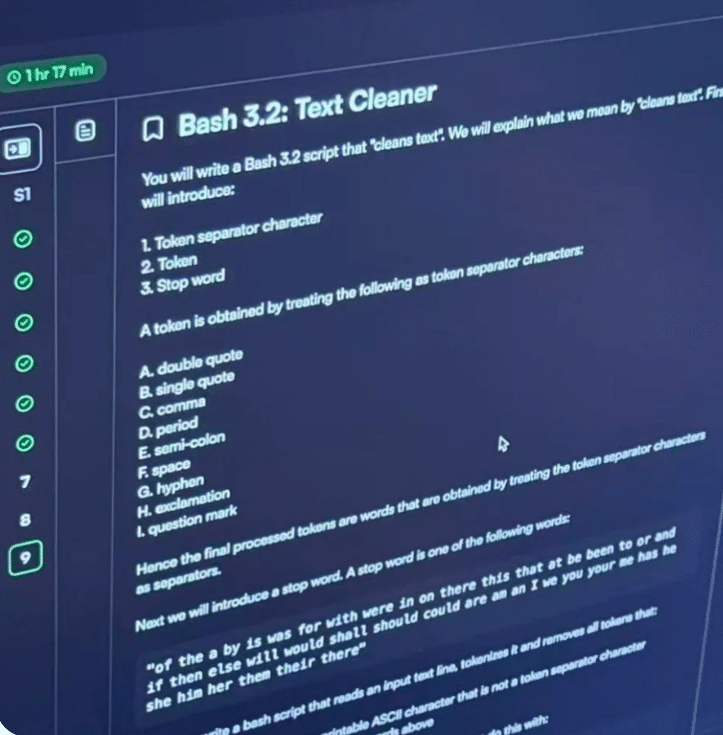
Q3: Text cleaning and word splitting
Introduction to the topic
Given multiple lines of input text, the text is required to be uniformly cleaned: ignore case, filter illegal characters, and split the processed text into word sequences for output.
Problem-solving ideas
This is a typical string processing question and can be completed according to a fixed process. First, all inputs are concatenated into a complete string and converted to lowercase uniformly. Then use regular expressions to replace all non-letter and non-numeric characters with spaces. Then split it using spaces as delimiters to get a preliminary word list. Finally, filter out the empty strings generated during the splitting process and output the remaining words. The overall process is clear and tests proficiency in strings and regular expressions.
Intuit OA& Full interview assistance service
Intuit's OA and interview process may not seem complicated, but what really eliminates people is often not "not being able to write questions" but time allocation, stuck ideas, and mistakes in details. We have long-term follow-up on the OA and VO processes of Intuit SDE / DS / NG positions, and provide real-time, low-interference, and stable interview assistance support based on their high-frequency question types and real screening logic.


