DRW 2026 Summer Quant/QR Intern OA 現已全面啟動!今年的OA延續了 DRW 一貫的“硬核”風格:題量大、時間緊、容錯率低。除了常規的程式設計題外,數學推理、機率統計以及經典的 Brainteasers(智力題)依然是考察重點。
很多同學初次上手時,往往因為時間分配不當或被某個“腦筋急轉彎”卡住而自亂陣腳,導致在細節上失分。目前我們已協助多位學員順利透過 DRW OA,實戰驗證表明:精準的解題策略和考點點撥,是提升效率、確保正確率的關鍵。 拒絕盲目刷題,有的放矢才能穩操勝券!

主要業務
DRW 的業務主要聚焦於三個領域:
- 流動性提供 Liquidity Providing
- 風險承擔 Risking Taking
- 低延遲交易 Latency Sensitive Trading
DRW 的 OA 還是挺難的,45 分鐘 6 個數學題,時間還是很緊的,下面一起來看下 DRW intern oa 25 summer 的真題。
問題 1
硬幣正面向上的概率為 0.8,反面向上的概率為 0.2,所以如果你選擇正面,每次翻轉為正面的概率為 0.8。 在 100 次翻轉中,預期的正面次數為 100×0.8=80,每次正面都會獲得$80。
問題 2
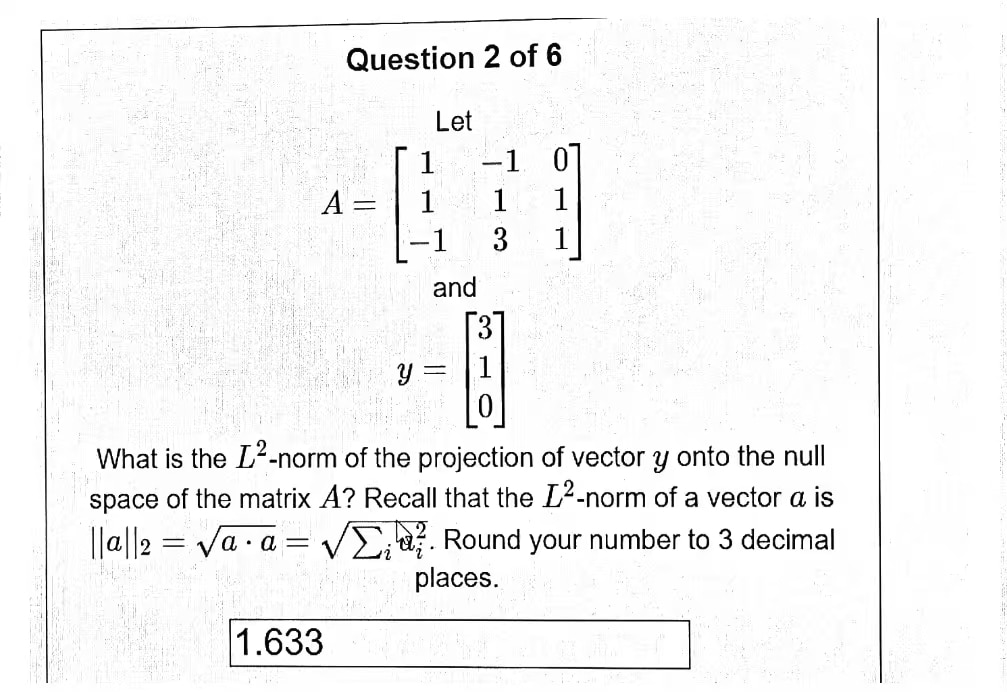
首先確定矩陣 A 的零空間,然後計算 y 到這個空間的投影,最後找出這個投影的 L2-範數。
問題 3

題目要求找到一個常數 c 來最小化量化誤差,這題可以直接寫 Python 代碼來解決,套公式:
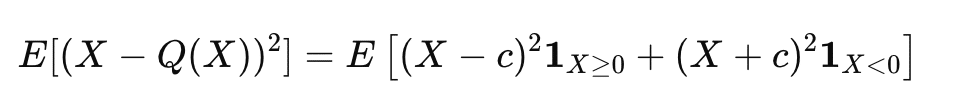
from scipy.optimize import minimize
from scipy.stats import norm
# 定义要最小化的目标函数
def quantization_error(c):
# 正态分布的参数
mean = 0
variance = 3
std_dev = variance**0.5
# 误差计算
# 对于 x >= 0, 计算 (x - c)^2,对于 x < 0, 计算 (x + c)^2
error_positive = lambda x: (x - c)**2 * norm.pdf(x, loc=mean, scale=std_dev)
error_negative = lambda x: (x + c)**2 * norm.pdf(x, loc=mean, scale=std_dev)
integral_positive = norm.expect(error_positive, loc=mean, scale=std_dev, lb=0, ub=np.inf)
integral_negative = norm.expect(error_negative, loc=mean, scale=std_dev, lb=-np.inf, ub=0)
return integral_positive + integral_negative
result = minimize(quantization_error, x0=0.5)
optimal_c = round(result.x[0], 3)
optimal_c問題 4

每次在看到 6 個不同面後擲出已投出面的概率是 6/7。 設 E 為總期望次數,解遞推方程即可,得到遞推公式:
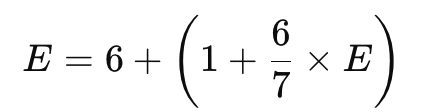
問題 5

這裡每次擲硬幣,根據硬幣正反面的結果,向前移動 1 步或 2 步。 我們需要計算 Pn,即“最終到達第 n 步的概率”,並特別求出 P4和P10的值,然后计算 1000(p4+p10)。
參考資料
DRW intern oa 25 summer | 一亩三分地
在我們的筆試輔助下,候選人成功完成了 DRW Intern 的 OA,並順利拿到了面試機會,如果你也需要 OA 輔助、面試輔助、代面,請聯絡我們。

